常微分方程式の精度保証

概要

常微分方程式の精度保証をするには、まずプログラムを生成する関数を実行し、次に生成したプログラムを実行するための関数を呼び出すという手順を踏む必要がある。常微分方程式を解くための方法は、今のところAffine Arithmeticを利用する方法とLohner法を利用する方法の2通りが実装してある。

方程式の記述には、Symbolic Math Toolboxを使う方法と使わない方法の2通りの方法がある。

関数と列挙型の一覧

使い方の詳細は「利用方法」に。

make_kv_maffine2(name, f, u, parameters[, compiler])

kv::ode_maffine2を利用するプログラムを生成、コンパイルする。[]で囲まれた引数は省略可能である。

  • name - 方程式の名前。
  • f - 方程式を並べたベクトル。
  • u - 変数を並べたベクトル。
  • parameters - パラメータを並べたベクトル。
  • compiler - 使用するコンパイラ。省略可。省略した場合はtools.detect_compiler()を使ってコンパイラを探す。
kv_maffine2(name, t_init, t_last, n, order, u, parameters, ep_reduce, ep_limit)

make_kv_maffine2()で作ったプログラムを実行して計算結果を返す。数値を受け取る引数には浮動小数点数、intval、文字列のいずれを渡しても良い。

  • name - make_kv_maffine2()に渡した方程式の名前。

  • t_init - 時間の始点だが、今は無視される(何を渡しても0が渡されたと見做す)。

  • t_last - 時間の終点。

  • n - \(t\)の分割数。\([t_{init},t_{last}]\)をn等分する。

  • order - Taylor展開の次数。

  • u - 初期値\(\mathbf{u}(0)=\mathbf{u}_0\)。

  • parameters - パラメータを並べたベクトル。

  • ep_reduce - Affine Arithmeticのダミー変数の上限値。kvの解説のep_reduceと同じ。

  • ep_limit - kvの解説のep_reduce_limitと同じ。「ダミー変数がep_limit個を超えたらep_reduce個まで減らす」という動作になる。

  • 戻り値[status, data, affine]

    statusは計算が正しく行えたかを表す。Status.SucceededかStatus.Incompleteのどちらかになる。

    dataは計算結果を表すintval型の行列。data(:, 1)(1番左の列)は各時間分点の値で、2列目はu(1)、3列目はu(2)、…を表す。 status == Status.Succeededの場合に行数 == n + 1でdata(end, 1) == t_lastとなる。status == Status.Incompleteの場合は 行数 < n + 1でdata(end, 1) < t_lastとなる。

    affineは\(t = \mathtt{data(end, 1)}\)でのuを表現するAffine多項式を表す行列。列数はuの列数と一致する。1行目はAffine多項式の定数項で、\(n(n>1)\)行目は\(n-1\)番目のダミー変数の係数となる。tools.plot_affine()にそのまま渡してプロットできる。

make_kv_qr_lohner(name, f, u, parameters[, compiler])

kv::odelong_qr_lohnerを利用するプログラムを生成、コンパイルする。引数はmake_kv_maffine2()と同じである。

kv_qr_lohner(name, t_init, t_last, order, u, parameters)

make_kv_qr_lohner()で作ったプログラムを実行して実行結果を返す。引数はkv_maffine2()と同様である。戻り値は[status, data]の2つで、これもkv_maffine2()と同様である。

Status

計算の成否を表す列挙型。次の3つの値がある。

Status.Succeeded

計算が最後まで正しく行えたことを表す。

Status.Incomplete

計算を始めることはできたが、途中までしか計算できなかった(途中で区間が発散した)ことを表す。

Status.Failed

出力用のファイルが開けなかったりして計算を始めることができなかったことを表す。生成したプログラムがこのステータスを返したとき、kv_maffine2()とkv_qr_lohner()はエラーを発生させる。

利用方法

Affine Arithmeticを使う場合

Lorenz方程式

\[\begin{split}\mathbf{u}= \begin{pmatrix} x \\ y \\ z \end{pmatrix}, \frac{d\mathbf{u}}{dt}= \mathbf{f}= \begin{pmatrix} \sigma (y - x) \\ x (\rho - z) - y \\ x y - \beta z \end{pmatrix}\end{split}\]

を例にしてライブラリの利用方法を説明する。今の場合\(x, y, z\)が変数で\(\sigma, \rho, \beta\)がパラメータである。

プログラムの生成

make_kv_maffine2()関数を呼び出してkv::ode_maffine2を利用するプログラムを生成する。

各引数の渡し方

  • name

    'lorenz-maffine2'などの文字列を渡す。

  • f

    Symbolic Math Toolboxを使う場合は次のfのようなシンボリック変数を使った式を並べたベクトルを渡す。

    syms x y z sigma rho beta;
f = [
    sigma * (y - x);
    x * (rho - z) - y;
    x * y - beta * z
];

    Symbolic Math Toolboxを使わない場合は次のfのような文字列のセル配列を渡す。

    f = {
    'sigma * (y - x)';
    'x * (rho - z) - y';
    'x * y - beta * z'
};

  • u

    Symbolic Math Toolboxを使う場合は次のuのようなシンボリック変数を並べたベクトルを渡す。

    syms x y z;
u = [x; y; z];

    Symbolic Math Toolboxを使わない場合は次のuのような文字列のセル配列を渡す。

    u = {'x'; 'y'; 'z'};

  • parameters

    uと同様にシンボリック変数のベクトルか文字列のセル配列を渡す。

  • compiler

    @compilers.msvcのようにコンパイラをラップした関数を渡すか省略する。

Symbolic Math Toolboxを使う場合の引数の例
syms x y z sigma rho beta;

f = [
    sigma * (y - x);
    x * (rho - z) - y;
    x * y - beta * z
];
u = [x; y; z];
parametes = [sigma; rho; beta];

make_kv_maffine2('lorenz-maffine2', f, u, parameters);
Symbolic Math Toolboxを使わない場合の引数の例
f = {
    'sigma * (y - x)';
    'x * (rho - z) - y';
    'x * y - beta * z'
};
u = {'x'; 'y'; 'z'};
parameters = {'sigma'; 'rho'; 'beta'};

make_kv_maffine2('lorenz-maffine2', f, u, parameters, @compilers.msvc);

エラーが発生しなければコンパイルに成功している。

プログラムの実行

プログラムの実行にはkv_maffine2()を利用する。

t_last = 50.0;
n = 5000;
p = 10;
init = [1; 0; 0];
parameters = [10; 28; intval(8) / 3];

[status, data, affine] = kv_maffine2( ...
    'lorenz-maffine2', 0.0, t_last, n, p, ...
    init, parameters, 120, 130 ...
);

次のようにすれば近似解をプロットできる。

plot3(mid(data(:, 2)),mid(data(:, 3)),mid(data(:, 4)));
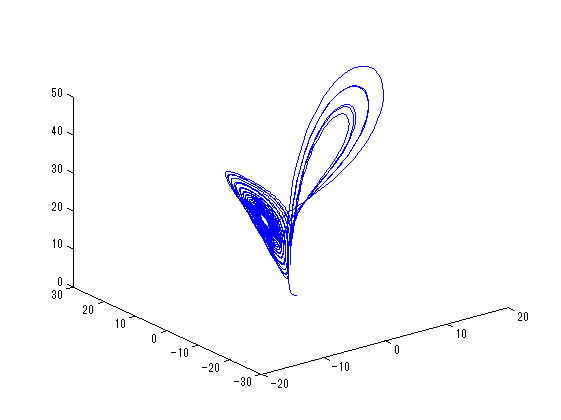
../_images/kv_maffine2_approx.png

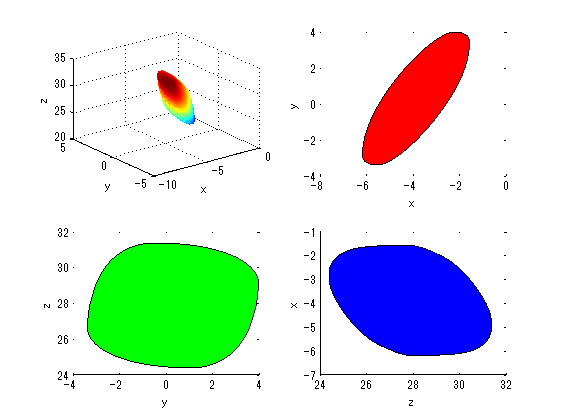
次のようにすれば\(\mathbf{u}(t_{last})\)を表すAffine多項式の構造を見ることができる。

figure;
subplot(2, 2, 1);
tools.plot_affine( ...
    a(:, 1), a(:, 2), a(:, 3), ...
    'FaceColor', 'flat', 'EdgeColor', 'none' ...
);
xlabel('x');
ylabel('y');
zlabel('z');

subplot(2, 2, 2);
tools.plot_affine(a(:, 1), a(:, 2), 'FaceColor', 'r');
xlabel('x');
ylabel('y');

subplot(2, 2, 3);
tools.plot_affine(a(:, 2), a(:, 3), 'FaceColor', 'g');
xlabel('y');
ylabel('z');

subplot(2, 2, 4);
tools.plot_affine(a(:, 3), a(:, 1), 'FaceColor', 'b');
xlabel('z');
ylabel('x');
../_images/kv_maffine2_affine_1.png

Lohner法を使う場合

Affine Arithmeticと大体同じ